什么是最小角定理

最小角定理是几何学中的一个重要定理，它描述了在一个三角形中，从顶点到对边的高与对边之间的角度是最小的。这个定理在几何证明和解决问题中有着广泛的应用。

最小角定理的定义

最小角定理可以这样定义：在一个三角形ABC中，设A、B、C为三角形的三个顶点，a、b、c分别为对边，从顶点A向边BC作垂线AD，那么∠ADB是三角形ABC中的最小角。

最小角定理的证明

要证明最小角定理，我们可以使用反证法。假设在三角形ABC中，∠ADB不是最小的角，即存在∠ADC

最小角定理的应用

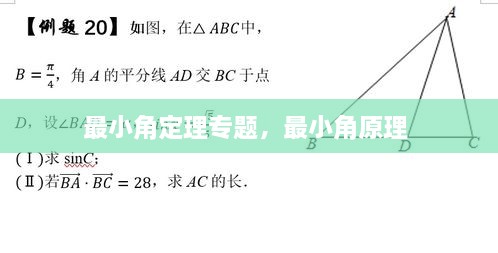
最小角定理在几何学中有许多应用，以下是一些例子：

• 在证明三角形的外接圆的性质时，最小角定理经常被使用。例如，在证明三角形的外心到三角形的三个顶点的距离相等时，可以利用最小角定理来证明。

  

• 在解决几何问题时，最小角定理可以帮助我们找到最优解。例如，在求解某些角度问题时，我们可以通过应用最小角定理来找到最小的角度值。

• 在建筑设计中，最小角定理可以帮助工程师设计出更加合理的结构。例如，在考虑建筑物的稳定性时，可以通过最小角定理来评估建筑物在各个方向上的角度。

最小角定理与其他几何定理的关系

最小角定理与许多其他几何定理有着密切的关系。以下是一些例子：

• 与勾股定理的关系：在直角三角形中，最小角定理可以帮助我们证明勾股定理。

• 与余弦定理的关系：最小角定理可以帮助我们推导出余弦定理的一个特例。

• 与正弦定理的关系：在解决涉及到三角函数的问题时，最小角定理可以与正弦定理结合使用。

  

最小角定理的实际意义

最小角定理不仅仅是一个数学定理，它在实际生活中也有着重要的意义。以下是一些实际应用的例子：

• 在建筑设计中，最小角定理可以帮助工程师设计出更加稳定和安全的结构。

• 在导航和地图制作中，最小角定理可以帮助确定方向和距离。

• 在物理学中，最小角定理可以帮助我们理解光的折射和反射现象。

总结

最小角定理是几何学中的一个基本定理，它揭示了三角形中角度与边的关系。通过证明和应用最小角定理，我们可以更好地理解三角形的性质，并在解决几何问题和实际问题中发挥重要作用。最小角定理不仅丰富了我们的数学知识，也在实际生活中有着广泛的应用价值。